Week of the 28/12/2020 - #53

Contents

Tech

• TIC80 interference effects

TIC80 interference effects

Finishing the year I played around with coding demo effects on the TIC80. I started from this effect and tried to get it first to fit in 256b which I was able to get down to 193b or 159 with compression with this code:

m=math
function n(x,y,a)
  return m.sqrt((m.sin(a)*100+120-x)^2+(m.cos(a)*34+68-y)^2)//1&8
end
function TIC()
  q=time()/1500
  for j=0,135 do
    for i=0,240 do 
      pix(i,j,n(i,j,q-2)-n(i,j,q))
    end
  end
end

which yields:

I tried in many ways to get it down to 128b but had no success. So I started tweaking the effect and came across some interesting variations based on it. This is one I like which has a nice transcient at the beginning:

m=math
function n(x,y,a)
  return ((m.sin(a)*90-x)^2+(m.cos(a)*90-y)^2)//2^10&8
end
function TIC()
  q=time()/1500
  for o=0,5^6 do i=o%120 j=o//360
    poke(o,n(i,j,q*1.2-i*m.exp(-q))-n(i,j,q))
  end
end

Which yields a nice sequence:

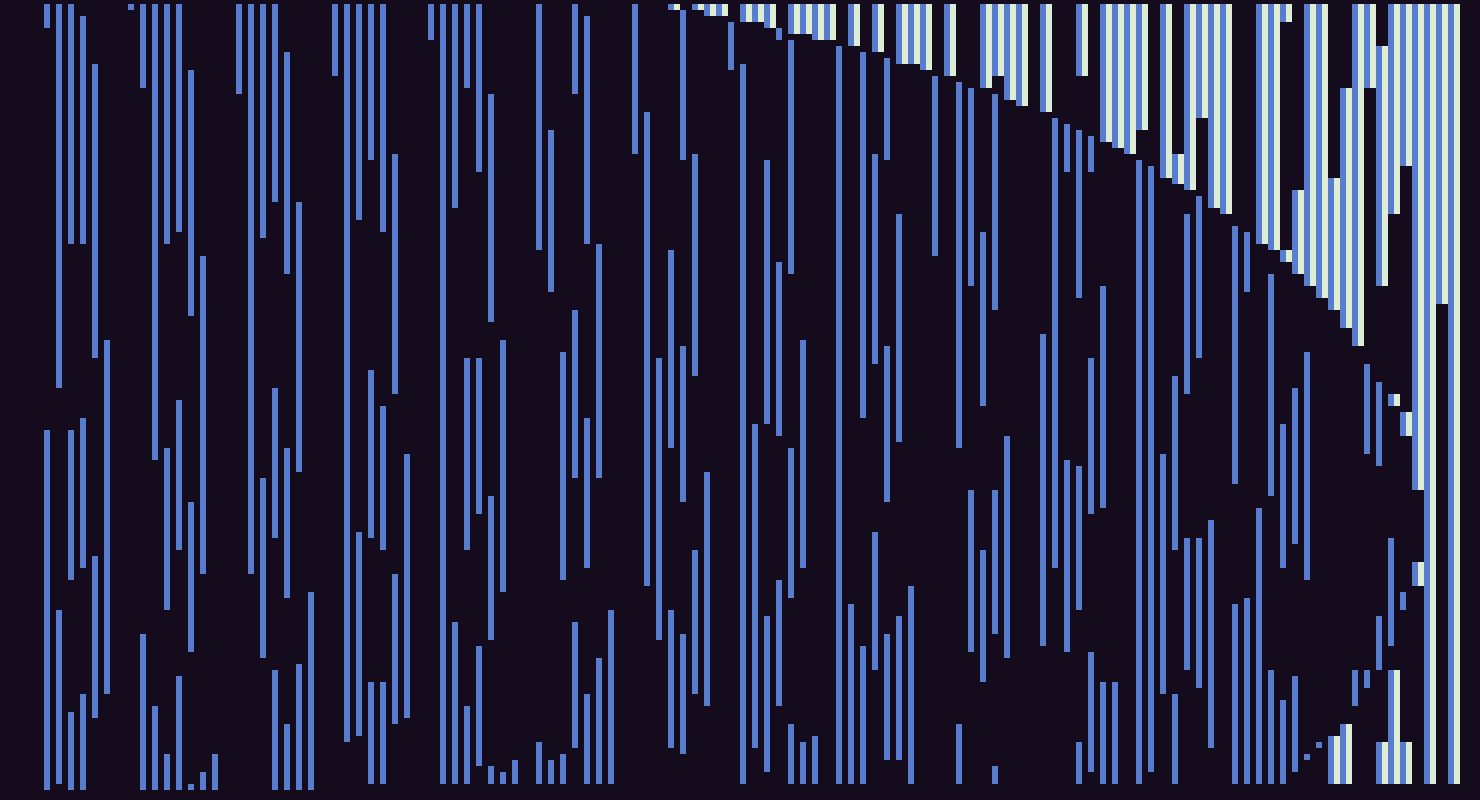
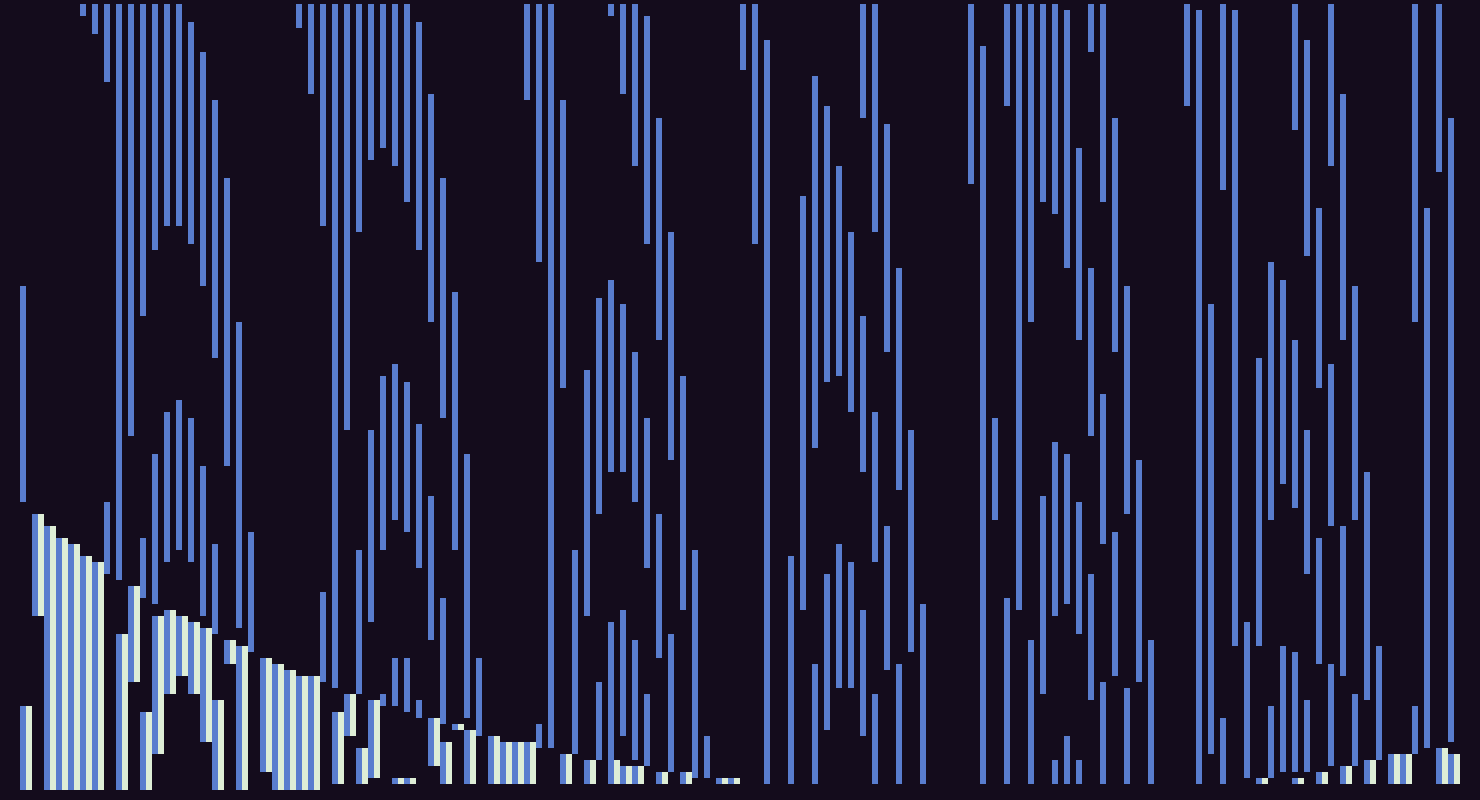
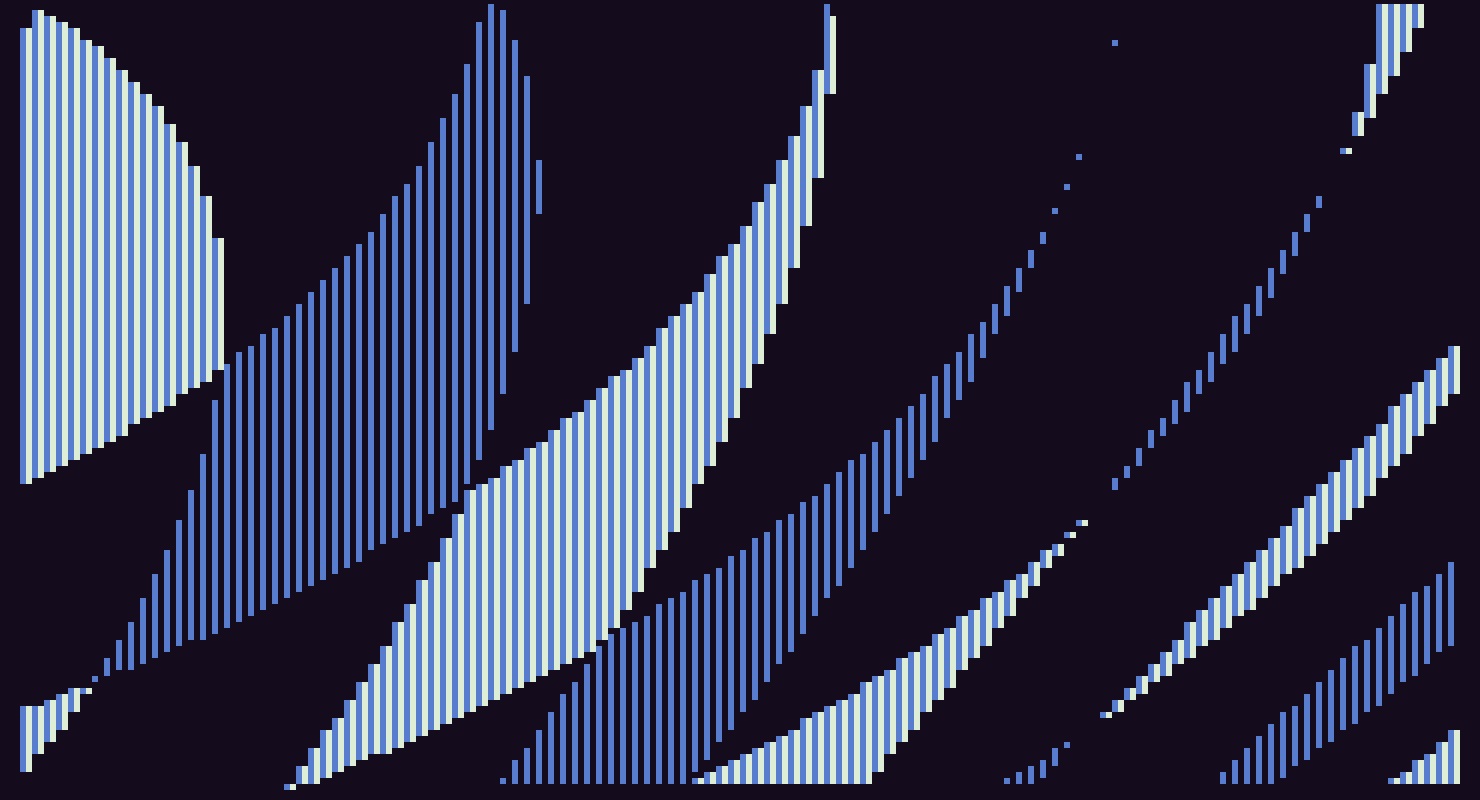
You can make it a little more periodic by adding a sin(q) in the exponential:

m=math
function n(x,y,a)
  return ((m.sin(a)*90-x)^2+(m.cos(a)*90-y)^2)//2^10&8
end
function TIC()
  q=time()/1500
  for o=0,5^6 do i=o%120 j=o//120
    poke(o,n(i,j,q*1.2-i*m.exp(-5*m.sin(.5*q)))-n(i,j,q))
  end
end

The smallest I could get with something nice is this (155 bytes compressed):

m=math
function n(x,y,a)
  return ((m.sin(a)*90-x)^2+(m.cos(a)*90-y)^2)//2^10&8
end
function TIC()
  q=time()/1500
  for o=0,5^6 do i=o%120 j=o//120
    poke(o,n(i,j,q*1.2)-n(i,j,q))
  end
end

This one also is pretty nice:

function n(x,y,a)
  return ((math.sin(a)*90-x)^2+(math.cos(a)*90-y)^2)//2^10&8
end
function TIC()
  q=time()/1500
  for o=0,2*5^6 do i=o%240 j=o//240
    poke4(o,n(i,j,q*1.2)-n(i,j,q))
  end
end