Week of the 07/12/2020 - #50
Contents
Science
- The “busy beaver” problem and its relation to math
Art
- Escher and an 8-bit demo
- Twitter likes
The “busy beaver” problem and its relation to math
One idea that has been circling in my mind for years is the posibility of proving mathematical theorems by showing that a particular program halt. Its straightforward to see that you can encode some mathematical theorems into programs that will stop if and only if the theorem is true. So if, by inspecting the program you somehow come to the conclusion it will have to stop under some condition then that would be equivalent of proving the mathematical theorem. Of course its not by any means obvious how to do this but it might turn out that its easier to prove the theorem in this other way.
Related to this idea is the “busy beaver” problem. The problem can be stated in the following way in terms of a Turing machine: given a Turing machine with a finite amount of states and a blank tape what is the halting program that can run the longest. More precisely, the busy beaver game consists of designing a halting, binary-alphabet Turing machine which writes the most 1s on the tape, using only a given set of states. The rules for the 2-state game are as follows:
- the machine must have two states in addition to the halting state, and
- the tape initially contains 0s only.
A player should conceive a transition table aiming for the longest output of 1s on the tape while making sure the machine will halt eventually.
The busy beaver question is interesting because if you know what is the longest a program of a particular size can run for then you know how long you have to wait to see if any other program of the same size will halt or not. By encoding a mathematical theorem in a program of that size you know how long you need to wait to see if its true or not. This week there was a great article on Quantamagazine on this topic. Here are some interesting links and papers relating to this problem:
- A 27-rule Turing machine that halts if — and only if — the Goldbach conjecture is false.
- The Determination of the Value of Rado’s Noncomputable Function 2(k) for Four-State Turing Machines - Deals with the k = 4 state problem.
- Attacking the Busy Beaver 5: An attach on the k = 5 problem which finds that it can write 4098 ‘1’s and runs for 47,176,870 steps. Postscript file
- Busy beaver competition and Collatz-like problems - This paper relates some of the longes running turing machines with Collatz like programs.
- The Simple Math Problem We Still Can’t Solve - A great article on the Collatz conjecture: a deceivably simple statement in mathematics.
Escher and an 8-bit demo
This week I spent some time watching and reading about Escher’s fascination of tilings. I’ve been a fan of Escher for many years and love his art. I have a book which is called “MC Escher: his life and complete graphics work”. In it I learned that he had written a book called “The regular division of the plane”. It was commissioned to hime by the De Roos Foundation and was printed in a limited number of copies. In it he describred his process for the creation of the regular division of the plane and created some beatufiul woodcuts to help the reader.



These two figures are also very illuminating:

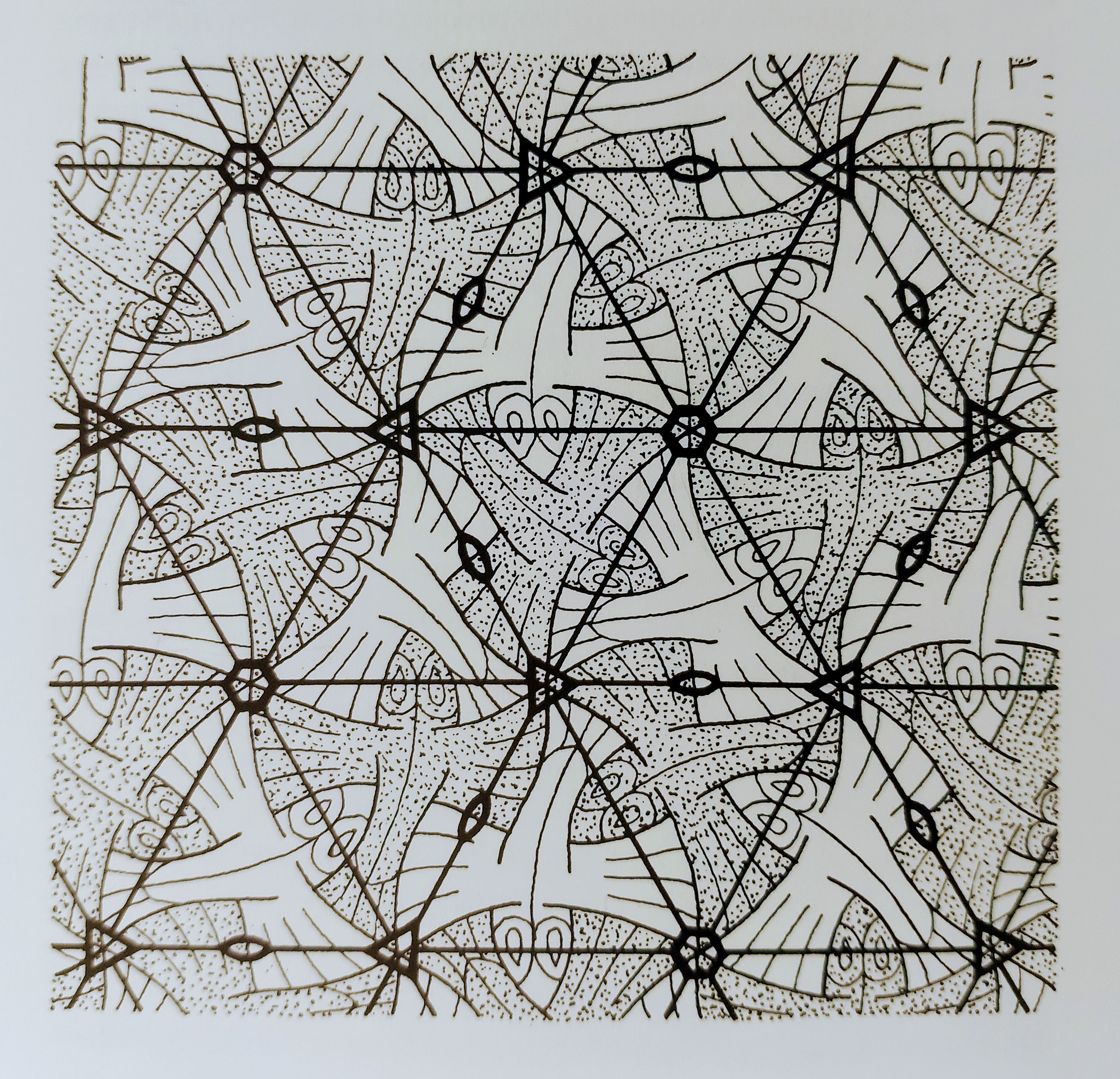
Inspired by his work I’m thinking about doing a demo for the Apple II by subdivision of the plane. I’ve already created some simple patterns and now I want to create more and combine them to make something inspire by woodcut I or by the famous “Metamorphosis II” print where the patterns combine one after the other:

So far I’ve been working in a Jupyter notebook to create the base patterns and then try to combining in a way that looks nice. Here are some of the patterns:
Pattern 1: standard checkerboard

Pattern 2

Pattern 3: 2 & 3 are from “Pattern in Islamic Art: Geometric Patterns & Borders”

Pattern 4: don’t rememeber where I saw this

And here is one possible way to combine them:

Here’s the source-code for this experiment:
import matplotlib.pyplot as plt
import matplotlib
import numpy as np
import math
cmap = matplotlib.colors.ListedColormap([[0.2,0.2,0.2], "white"])
# Vacio
def pattern0(row, col):
offset = 6
if row < offset:
return 0
p = 0.18 * math.sqrt(row - offset)
if np.random.random_sample() < p:
return pattern1(row,col)
return 0
# patron cuadriculado
def pattern1(row, col):
row = row % 4
col = col % 4
if row < 2 and col < 2:
return 1
if row > 1 and col > 1:
return 1
return 0
# patron arabesco 1
def pattern2(row, col):
row = (row - 3) % 4
col = (col - 1)% 4
if row == 0 and col == 1:
return 1
if row == 1 and col > 0:
return 1
if row == 2 and col < 3:
return 1
if row == 3 and col == 2:
return 1
return 0
# patron cruces desfazadas
def pattern3(row, col):
pattern = "" + \
"0010111010" + \
"0111010001" + \
"1010001011" + \
"0001011101" + \
"1011101000" + \
"1101000101" + \
"1000101110" + \
"0101110100" + \
"1110100010" + \
"0100010111"
row = (row) % 10
col = (col) % 10
index = row * 10 + col
c = pattern[index]
if c == '0':
return 0
return 1
# patron cruces desfazadas
def pattern4(row, col):
pattern = "" + \
"0100" + \
"1110" + \
"0111" + \
"0010"
row = (row) % 4
col = (col) % 4
index = row * 4 + col
c = pattern[index]
if c == '0':
return 0
return 1
width = 16
height = 100
bits = np.zeros((height,width))
for row in range(0, height):
for col in range (0, width):
if row < height / 4:
color = pattern0(row, col)
elif row < height / 2:
color = pattern1(row, col)
elif row < height * 3 / 4 - 3:
color = pattern2(row, col)
else:
color = pattern3(row, col)
bits[row][col] = color
plt.figure(figsize=(15,30))
plt.xticks([0,15],['0', '0xf'])
plt.yticks([0,15],['0', '0xf'])
plt.axis("off")
plt.imshow(bits, interpolation='none', cmap=cmap, origin='upper' )
Links & ideas
- For the Apple demo, one idea is to generate a bitmap with all the combined patterns and use a compressor like lzsa to compress it and scroll it from bottom to top. The demo can be stored on disk using qboot for its speed and/or c2d to create a bootable disk.
Twitter likes
Here is some visual stimulation I’ve collected from my Twitter like feed:











